How to Read a Probability Density Function Graph
Interpreting the Probability density functions every bit a data scientist
Random variable:
Detached random variable: X is a discrete random variable, if its range is countable.
Continuous random variable: A continuous random variable is a random variable where the data tin can accept infinitely many values. For instance, a random variable measuring the time taken for something to be done is continuous since at that place is an space number of possible timestamps that can be taken.
Population and sample:
- A population includes all of the elements from a set of data. Hateful of the population is denoted as μ.
- A sample consists of ane or more than observations fatigued from the population. The mean of the sample is denoted as X̄. If sampling was done randomly than information technology is called a random sample.
Every bit sample size increases, the sample ways converges to the population mean.
Depending on the sampling method, a sample tin can have fewer observations than the population, the aforementioned number of observations, or more observations. More than ane sample tin be derived from the same population.
Gaussian distribution(Normal distribution):
- The mean, median and fashion of the distribution coincide.
- The bend of the distribution is bell-shaped and symmetrical about the line x=μ.
- The total expanse under the curve is 1.
- Exactly half of the values are to the left of the middle and the other half to the right.
Most of the continuous random variables followed Gaussian distribution by nature. The probability density function can be shown below.
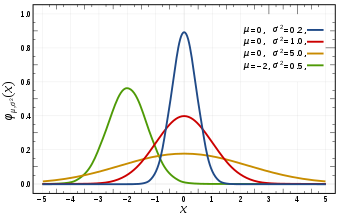
The height is generally located at the mean position of the population where σ² denoted variance of the population. σ² decides the shape of the PDF.
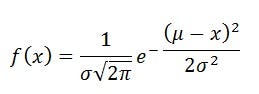
- As 10 increases(move away from μ), y reduces exponential of the squire.
- The curve is symmetric.
- Shape fall is exponentially quadratic.
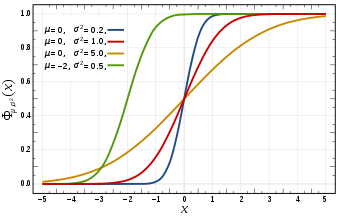
When mean = 0, all curves are at probability =0.5.
Equally the variance decreases, the curve tries to become vertical line at ten=0.
68–95–99.7 rule
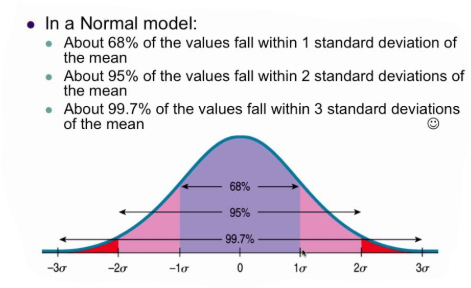
68% of the points lie between -1σ to 1σ deviation of the hateful.
Symmetric distribution, Skewness, and Kurtosis:
A symmetric distribution is a blazon of distribution where the left side of the distribution mirrors the right side. By definition, a symmetric distribution is never a skewed distribution.
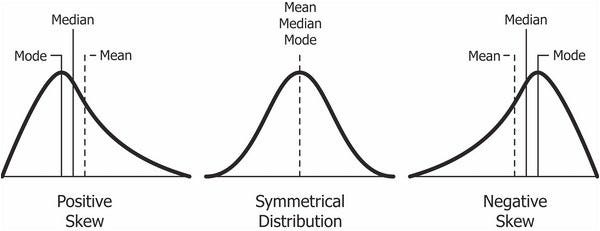
- Kurtosis measure the peakedness of a distribution.
- Mean gets impacted by outliers.
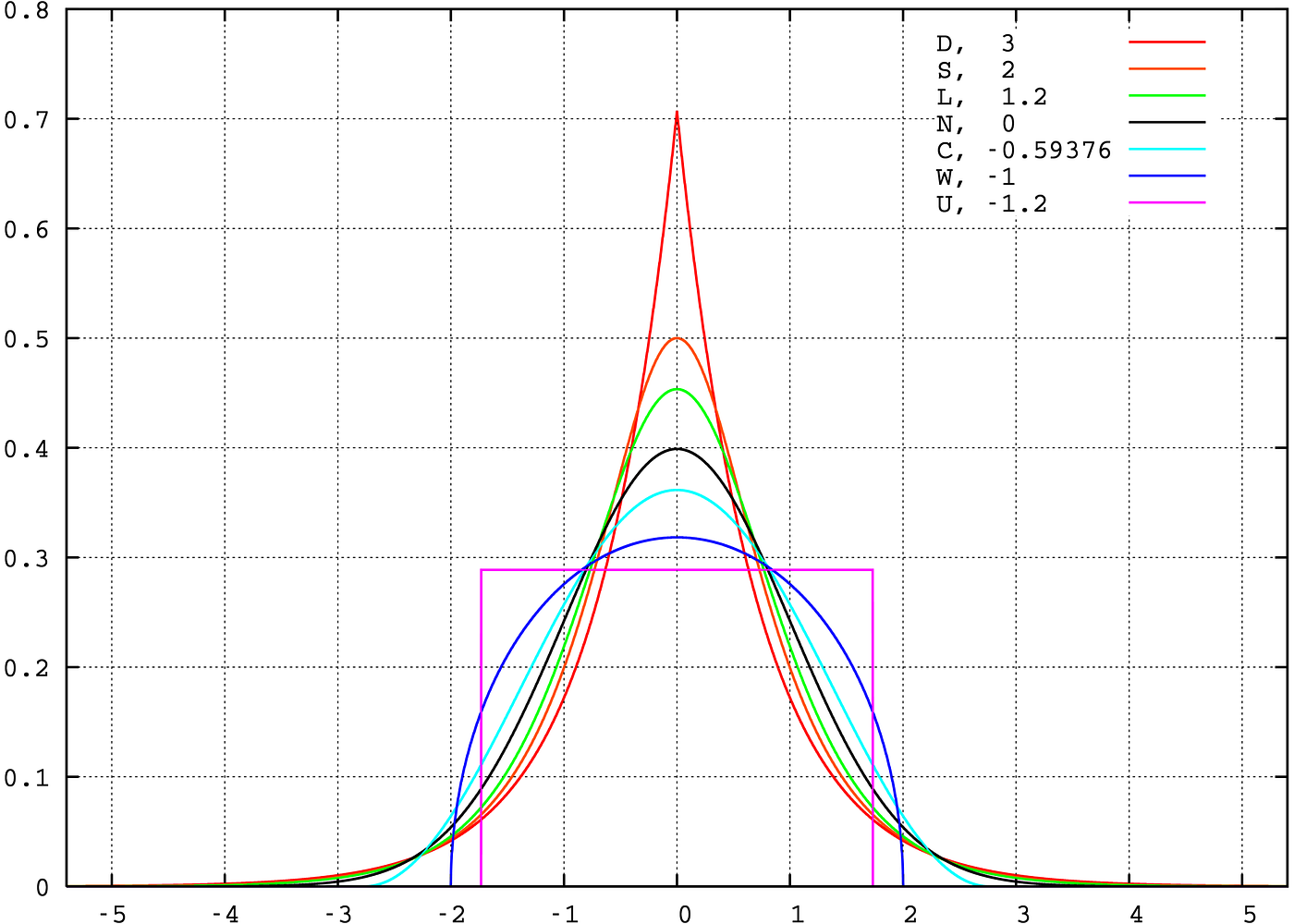
The bend above the normal plot is positive kurtosis and beneath the normal curve (North=0) is negative kurtosis.
Standard normal variate:
Given whatever distribution with given points (X1,X2,X3,X4..) with mean and variance = North(μ,σ²), you lot can standardize to convert into standard normal variate N(0,1).
After standardization, you lot can tell only the 68% of points lie betwixt -1 and +1. and 95% point lies between -2 to +2.
Kernel density estimation:
Used to catechumen histogram into PDF.
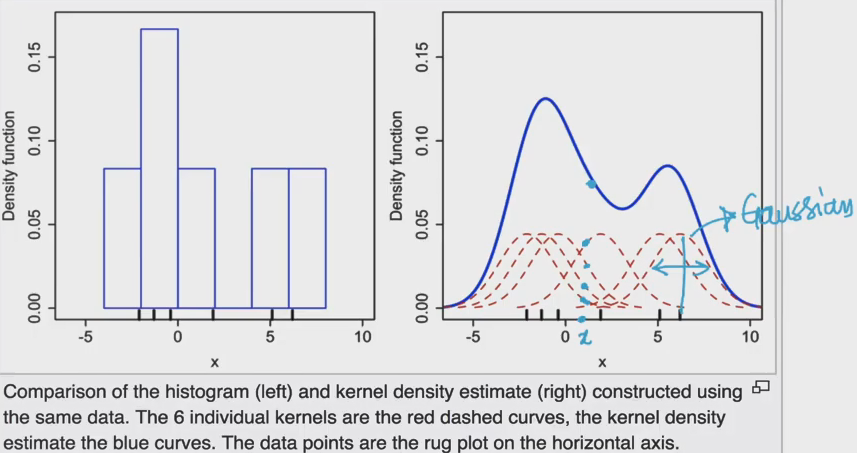
Accept all heights of points on individual kernels and sum them — the sum is total meridian of distribution.
Sampling distribution & Primal Limit theorem:
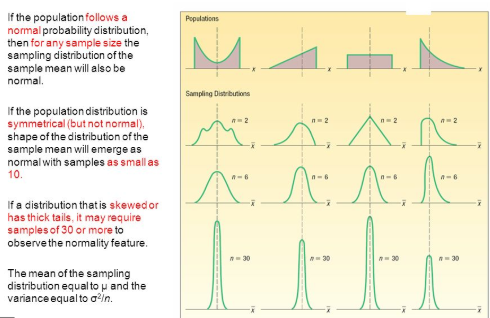
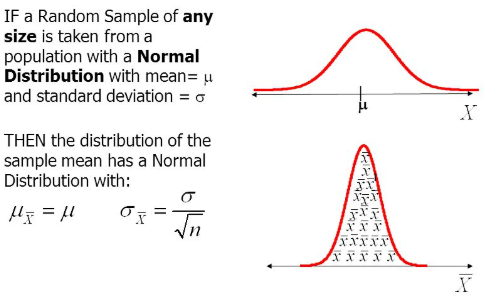
CLT: The means of each sample from the population is equal to the population mean(μ). The distribution can be any distribution.
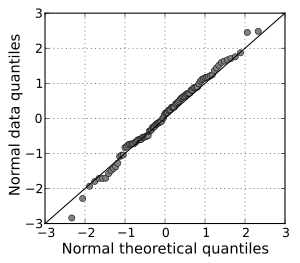
Quantile-Quantile plot(Q-Q plot):
To decide the random sample variables normally distributed or not. if the number of samples is small, it is had to translate the Q-Q plot.
How distributions are used?
Gaussian distribution requite the theoretical model of distribution of information which observed in many cases of natural miracle.
Suppose we know that data is distributed normally X ~ North (µ, σ) with mean µ and difference σ. Nosotros can draw PDF and CDF using the in a higher place random information.
PDF and CDF tell u.s.a. how data is distributed. PDF and CDF describe only in the case of Gaussian distribution.
Chebyshev'south inequality:
If I don't know the distribution, hateful=finite, and standard=finite. We can not draw PDF and CDF because of distribution.
Here y'all can find the per centum of points lying between the given range.

Uniform distribution:
It is used to generate a random number which has a lot of applications. Summit tells usa what the probability is of finding that value. The probability density function(PDF) for continuous random variable and probability mass role(PMF) for a discrete random variable:
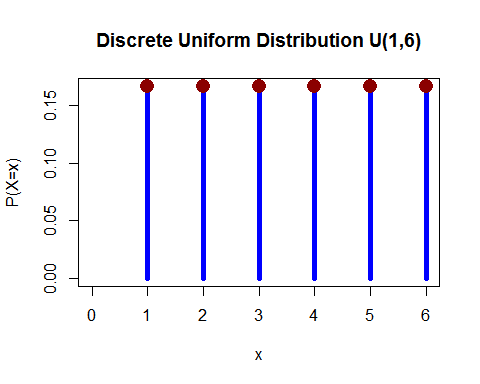

NOTE: sample uniformly means each point have equal take a chance of prevarication in sample dataset D'
Bernoulli and Binomial Distribution:
Log-Normal Distribution:
if ln(10) is normally distributed. if not, you can check using the Q-Q plot.
Annotation: if information given in log-normal, convert into Gaussian distribution past taking log. so you can use all ML techniques.
About of the time in the real application, distribution is log-normal. Log-normal is correct-skewed as we increase σ value. please run across the example given below link.
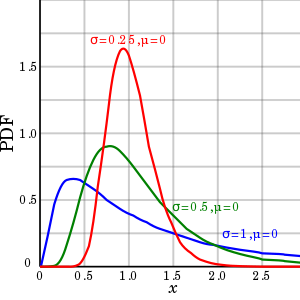
instance found at the below link.
Power police force distribution:
also know every bit eighty–20 rule. 80% of the time value found in a xx% interval.
Pareto distribution:
y'all tin can observe an case in the awarding section in the above link.
Box cox transform:
if the dataset is in power-constabulary/Pareto distribution, to catechumen into Gaussian distribution, use Box cox transform.
By putting all ten value in Box cox function, you will get lambda( λ) value. use lambda( λ) value you lot can catechumen each x into y.

you lot tin can directly find Y value using the formula given in link
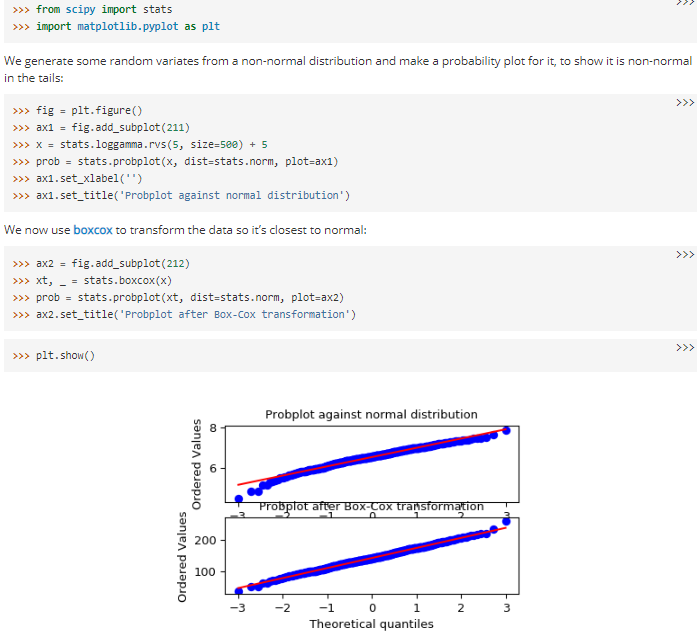
In a single line using boxcox(x) function, in just 1 line, we tin find y value which is normally distributed.
Weibull distribution:
Used to measure the top of the dam. collect a one-week interval of rain data.
to determine particle size
Source: https://medium.com/analytics-vidhya/interpret-as-data-scientist-of-the-probability-density-functions-32e933fa47c5
0 Response to "How to Read a Probability Density Function Graph"
Post a Comment